Meta分析中效应量及其相互转换

June 09, 2022

一、什么是效应量

效应量是用以衡量“效应”大小的指标，可以量化变量之间的关联程度，可以比较自身前后变化，也可以比较组间差异。效应量并非只是某一种指标，目前已经有超过100种效应量的概念被应用于统计领域，常见的均数差（MD），相关系数（r），相对风险度（RR），比值比（OR）等等都属于效应量。有些保留结果的原始单位，如均数差。有些对效应量进行标准化，如Cohen’s d，有些则无单位，如相关系数。下表根据效应量类型列举了一些常见的效应量类别、名称以及适用数据类型：

效应量类型	效应量名称	适用数据形式
Correlation (r-family)	Pearson $r$	Correlational data
	$R^{2}$ ( $r$ -squared)	Correlational data
	$η^{2}$ (Eta-squared)	Correlational data
	$ω^{2}$ (Omega-squared)	Correlational data
Difference (d-family)	Cohen’s $d$	Continuous data
	Hedges’ $g$	Continuous data
Categorical (OR-family)	Cohen’s $w$	Binary data
	Odds ratio (OR)	Binary data
	Relative risk (RR)	Binary data

二、效应量的意义

统计学家Gene V. Glass说：“统计显著性（statistical significance）是有关于结果最无聊的事情，你应该根据量化来描述结果——不光只是指出某种治疗对人会有影响，还应当告诉人们这种影响究竟有多大。”

2016年美国统计协会官方发布了一则声明，严肃讨论了 $p$ 值的内涵以及解释方法，旨在呼吁人们重视科学研究结论的可重复性问题，改变长久以来沿用的一些陈旧的统计推断实践。效应量可以弥补因为过度依赖 $p$ 值而造成的结果误判，如一项比较了某种治疗和安慰剂的研究结果可能具有极小的 $p$ 值（有统计学意义）但同时效应量也很小（无实际应用意义）。如果过度依赖p值描述结果，则无法反映差异的大小。此外，当样本含量很大的时候（如超大样本数据挖掘），显著性水平如果还保持在常用0.05的水平，则很容易检测出细微却又无实际意义的差异。

三、统计量与效应量以及效应量之间互相转换

在meta分析中为了统一效应量，可在不同效应量之间进行转换（下图）：

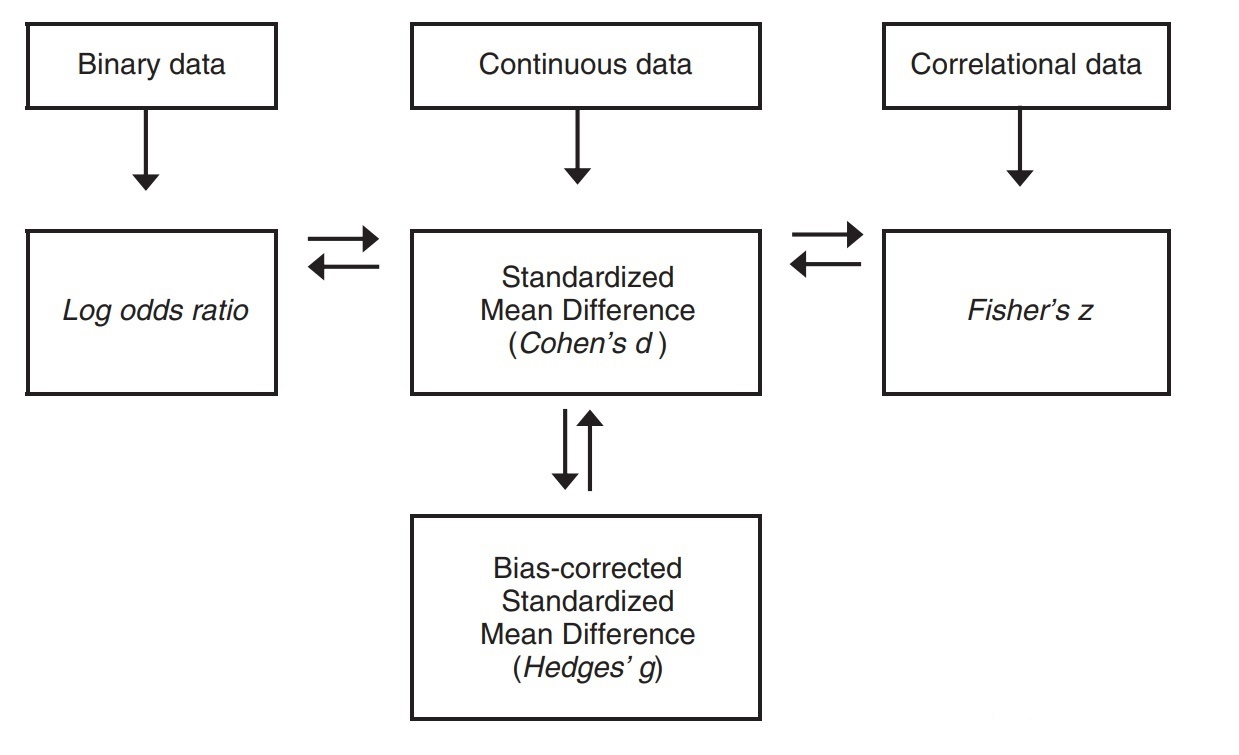
此外，由于很多文献（尤其是老文献）通常只报告统计量（如 $t$ 、 $F$ 、 $χ^{2}$ ）及其 $p$ 值，而且并不总能找到均值、标准差等原始的描述统计量，所以在做元分析的时候，我们需要把统计量转换为效应量。以下，为部分统计量与效应量以及效应量之间互相转换的公式：

Pearson’s $r$

$r = \sqrt{η_{p}^{2}} = \sqrt{\frac{f^{2}}{f^{2} + 1}} = \sqrt{\frac{d^{2}}{d^{2} + 4}} = \sqrt{\frac{t^{2}}{t^{2} + d f}} = \sqrt{\frac{F \cdot d f_{1}}{F \cdot d f_{1} + d f_{2}}} = \sqrt{\frac{λ^{2}}{N (k - 1)}}$

均需要加±，根据实际情况判断正负。
$r = β + 0.05 λ$ $β = (\frac{S D_{x}}{S D_{y}}) \times B$

$β$ is standardized regression coefficient, $λ$ is a constant that takes the value of 1 when $β$ is greater than or equal to zero, and a value of 0 when $β$ is smaller than zero, $B$ stands forunstandardized regression coefficient.
$r = 2 \sin (\frac{π}{6} r_{s})$

$r_{s}$ refers to Spearman’s $ρ$ .
$r = \sin (0.5 π τ)$

$τ$ is Kendall’s tau.
$r = \frac{\sqrt{O R} - 1}{\sqrt{O R} + 1}$

$O R$ indicates univariate odds ratios (ORs)

Cohen’s $d$

$d = \pm 2 f = \frac{2 r}{\sqrt{1 - r^{2}}} = t \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}} or {\frac{2 t}{\sqrt{N}}}_{(n_{1} = n_{2} = N / 2)}^{(独立样本)} = {\frac{t}{\sqrt{N}}}^{(配对样本)} = l n (O R) \cdot \frac{\sqrt{3}}{π}$

Note:

与 $O R$ 相关的转换存在一定的误差，主要在于 $\frac{π}{\sqrt{3}}$ 是二分类Logistic回归中因变量标准差的近似估计值。
关于不同效应量之间的相互转换，可参考一个在线小程序（[Computation of different effect sizes like d, f, r and transformation of different effect sizes: Psychometrica]）

Source:

[Peterson RA, Brown SP. 2005, On the use of beta coefficients in meta-analysis. J Appl Psychol]
[van Valkengoed, A.M., Steg, L. 2019, Meta-analyses of factors motivating climate change adaptation behaviour. Nature Clim Change]
[以Cohen’s d为例浅谈效应量（Effect size）]
[统计量–效应量的相互转换|元分析基础]